우리는 주변의 공간을 3차원으로 인식하고 3차원의 세계에서 사는 데 익숙해져 있다. 그래서 상식적으로 이해할 수 없는 사람을 일컬어 ‘4차원’에 있다고 놀린다. 사람들에게 4차원은 그만큼 낯설고 세상과 동떨어진 개념으로 여겨지는 것이다. 그런데 위상수학을 연구하는 박종일 교수(수리과학부)는 “우리가 사는 시공간, 나아가 우리가 몸담은 우주의 무수한 공간들이 4차원의 형태로 존재한다”고 말한다. ‘4차원 공간’을 꾸준히 연구하고 해당 분야를 발전시킨 점을 인정받아 2013년 대한민국 최고과학기술인상을 수상한 박 교수를 『대학신문』에서 만나봤다.

이름조차 생소한 ‘4차원 다양체’
일반인들에겐 이름조차 생소한 ‘4차원 다양체’라는 박 교수의 연구분야를 알기 위해선 ‘위상수학’이라는 세분화된 수학 전공과 수학사의 흐름을 이해해야 한다. 20세기 이후 수학은 대수학, 해석학, 기하학 등으로 분화, 발전했고 특히 기하학 분야에서도 연구의 성질에 따라 각기 다른 영역들이 발전했다. 공간의 부분 부분들을 파악함으로써 전체 공간의 성격을 이해하고자 하는 연구가 있었고, 반대로 부분보다는 공간의 전체적 성질을 파악하려는 연구도 있었다. 그 중 후자가 ‘위상수학’이라 불리는 박 교수의 전공분야다. 박 교수는 “전체 공간이 가지고 있는 공통적 성질을 탐구하는 것이 위상수학”이며 “4차원 다양체도 위상수학의 한 연구 주제다”고 말했다.
4차원 다양체의 한 예로 박 교수는 “팽창하는 풍선에 시간이라는 한 축을 더 얹은 것”을 들었다. 풍선 위를 걸어다니는 개미는 풍선을 2차원으로 인식하지만 표면 밖에서 풍선의 전체적인 모습을 보는 우리는 그것을 3차원으로 인식한다. 그런데 만약 시간이라는 축 밖에서 팽창하는 풍선의 전체적인 모습을 본다면 우리가 인지하지 못하는 4차원의 공간을 본다는 것이다. 박 교수는 “실제로 팽창하는 풍선의 예는 천문학자들이 우주를 보는 방식이며, 4차원 다양체의 가장 친숙한 예로 우리가 사는 시공간이 있다”고 말했다. 옛날 지구가 둥글다는 것을 알기 전엔 평평한 땅을 걸어가던 사람들은 지구를 2차원 공간으로 여겼을 것이다. 지금 우리가 우주에서 지구의 전체적 모습을 보고 그것이 3차원인 줄 아는 것처럼 우리가 사는 우주도 실제론 3차원을 넘어선 무수한 다양체들의 집합일 것이라는 수학적 추측이다.
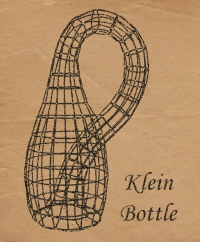
안과 밖이 없는 뫼비우스 띄의 3차원 형태다. 3차원에서 존재할 수 없음이 증명된 바 있다.
시공간은 4차원의 주요한 예시지만 박 교수의 연구 목표는 시공간외에도 4차원 다양체들의 여러 종류를 찾고 그것들을 분류하는 것이다. 이를테면 안과 밖의 구별이 없는 공간으로 잘 알려진 ‘클라인 병’(그림 ①) 외에도 가능한 4차원 다양체의 모습을 찾아내고 그 특성을 밝히는 것이다. 이번 수상의 주요사항인 난제 해결도 공간에 대한 꾸준한 연구가 뒷받침된 것이었다.
60년 동안의 난제를 풀다
대한민국 최고과학기술인상 수상의 주요한 이유 중 하나는 그동안 난제로 여겨졌던 ‘기하종수*가 0이고 음(-)의 곡률*을 갖는 단순연결 된 4차원 다양체 및 복소곡면*의 존재성 문제’를 해결했다는 것이다. 박 교수는 “쉽게 생각하면 ‘음으로 휘어진’ 4차원 다양체를 발견했다는 것이다”고 말하며 다소 전문적인 내용을 풀어 설명했다. 이 문제의 역사는 60년 전 이탈리아의 수학자 프란체스코 세베리의 4차원 다양체에 관한 한 추측에서 시작됐다. 그는 ‘기하학적 종수가 0이고 단순연결된 곡면은 평면과 거의 같다’고 추측했고, 이후 수십 년간 수학자들은 그 추측의 오류를 증명할 반례를 찾고자 했다. 즉 ‘기하학적 종수가 0이고 단순연결됐으면서도 평면과 같지 않고 곡률이 음인 공간’을 발견하고자 했다. 그러던 중 박 교수가 조건에 맞는 4차원 공간을 찾아내 주목을 받게 된 것이다. 박 교수는 “원래 해당 분야를 직접적으로 공부하고 있지 않았지만 당시 공부하고 있던 분야에서 새로운 아이디어를 얻을 수 있겠다는 생각을 했다”며 난제를 푼 과정을 소개했다.
박 교수가 제시한 새로운 아이디어는 ‘유리적 블로다운 수술*’이라는 위상적 이론과 ‘Q-고렌슈타인 매끄러움*’이라는 대수적 이론을 통합한 것이었다. 박 교수는 “쉽게 말하면 공간을 자르고 이어붙여 새로운 공간을 만드는 과정”이라고 다소 전문적인 용어를 소개했다. 그런 과정을 통해 만들어진 곡률이 음인 4차원 다양체는 ‘안으로 오목하게 생긴 구’이며 육안으로는 지각하기 힘들다. 박 교수는 또 한편으로는 “우연한 착안에 의해 조건에 맞는 공간을 찾았지만 아직 왜 그 공간이 조건에 맞아야 하는지 일반화하기 어렵다”며 여전히 미진한 부분을 설명하기도 했다. 이번 난제 해결은 새롭게 찾은 4차원 공간뿐만 아니라 그 독창적인 방법으로도 주목을 받으면서 앞으로 수학계에 다방면으로 활용될 것으로 보인다. 실제로 박 교수의 연구는 수학분야의 권위있는 학술지 「인벤쇼네스 마테마티케(Inventiones Mathematicae)」 2007년 12월호에 발표돼 생산적인 논의를 주도하기도 했다.
국제적 교류를 통해 연구 계속해나갈 것
박 교수에 대한 심사평 중에는 ‘4차원 다양체 분야를 개척, 발전시켜 한국의 연구 역량을 세계적인 수준으로 끌어올렸다’는 언급이 있다. 실제로 박 교수는 수학 분야의 가장 권위있는 학술행사인 2010년 국제수학자총회에서 국내 수학자로는 유일하게 초청연사로 선정됐으며, 2012년에는 미국수학회의 초대 석학회원으로 선정되는 등 국제적으로 활발히 교류하고 있다.
다방면의 노력과 성취에도 불구하고 기초학문의 특성상 가시적인 성과를 내기가 힘든 것이 현실이다. 수학자인 박 교수가 최고과학기술인상을 받게 된 것도 매우 드문 경우에 속한다. 때문에 이번 수상은 과학기술 분야의 원천이 되는 기초학문에 대한 새로운 평가로 비춰지기도 한다. 이에 박 교수는 “미래의 과학기술 및 사회의 발전을 위해 기초과학은 매우 중요한 것이다”고 말하는 한편 “의식적으로 내가 하고 있는 일의 목적성을 생각하기보단 본인이 하고 있는 업무에 대해서 최선을 다하는 것이 가장 중요하다고 생각한다”며 앞으로도 4차원 다양체 분야 관련 연구를 계속해나갈 것이라고 밝혔다.
* 기하종수 : 공간의 전체 모양을 규정짓는 불변량 중의 하나
* 곡률 : 공간이 휘어진 정도를 나타내는 수치
* 복소곡면 : 대수적 구조와 기하학적 구조를 동시에 갖고 있는 대표적인 4차원 공간
* 유리적 블로다운 수술(rational blow-down surgery) : 위상수학 분야에서 개발된 기술로 새로운 위상공간을 만드는 방법 중의 하나
* Q-고렌슈타인 매끄러움(Q-Gorenstein
smoothing) : 대수기하학 분야에서 개발된 변형이론으로 새로운 복소공간을 만드는 방법 중의 하나